How to Know Which Units to Use Related Rates

So it looks like. Because our rates are all in per minute.

Calculus I Related Rates

We can assign h to be the waters height so its rate of change will be dfrac dh dt where dt represents the change in time t.

. However by common sense d θ d t should be in o s if using degrees. Related rates problems will always tell you about the rate at which one quantity is changing or maybe the rates at which two quantities are changing often in units of distancetime areatime or volumetime. If we let denote the volume at time then the unknown quantity is.

This is the known information. It takes you 2 hours to. But heres where it can get tricky.

Examples of How to Find Unit Rate or. The rate youre after is related to the rate s youre given. Ii Write down the quantity you are trying to find - any related rates problem will be asking you to find some derivative.

We have done a lot of work in the land of Calculus but much of it has been based on abstract concepts and perfecting our calculation abilities. If r is a function of time with rate of change 1 cms then we can define this function as r t 3. 2 x d x d t 2 y d y d t 0.

As we see from square A is increasing not constantly. 2 x d x d t 2 y d y d t 0. V 1 3 π r 2 h.

Express the asking rate look for phrases such as how fast at what find the rate etc. 30 Points Related Rates and Derivatives in the Real World. 2 Determine what you are asked to solve.

The distance should be set as the numerator top number and the amount of time should be set as the denominator bottom number. If we divide both sides by negative 15 we get theta prime of T is equal to three over negative 15. This now gives us the revenue function in terms of cost c.

Three over negative 15. At this point all we need to do is plug in what we know and solve for h h. However Calculus has a rich history of being one of the most directly applicable forms of all mathematics.

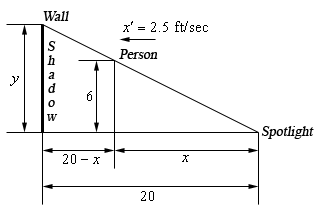
Divide the distance by the time as indicated reducing the denominator to one unit of time. Dthetadt there is an implied unit since this refers to the rate of change of the angle SIZE. 2 25 196 π 6 2 h h 98 225 π 01386 2 25 196 π 6 2 h h 98 225 π 01386.

Introduce the notation you will use. Write down the givens and unknowns from the question 5. Based on the actual problem youd label a triangle with a few sides and one of the angles as theta.

To find a relationship between the rates of change of x and y with respect to time we can implicitely differentiate the equation above with respect to t. So if I wanted to I could write radians per minute. Another way to find the unit rate is to measure how long it takes you to do something that has a known quantity.

To find the related rates ie. A π t 3² π t² 6π t 9. This is one of the key steps in related rates.

This is the general relationship between the speed of x and y. Is the unit degrees or radians. In general the best way to approach a related rates formula is to use the following steps.

Imagine that you had a friend who lived 100 miles away. The question will then be. Because we were given the rate of change of the volume as well as the height of the cone the equation that relates both V and h is the formula for the volume of a cone.

I Introduce all relevant variables and draw a picture to describe what is going on. The formulas for revenue and cost are. Read and understand the problem 2.

Mark the radius as the distance from the center to the circle. You need to read the problem and identify what you are being asked to solve. If we let denote the length of an edge of a cube at time then we can write.

Any related rates problem consists of two or more changing elements as well as any number of constant terms that will have some bearing on the answer. Draw a diagram in most cases 3. θ is a ratio it has no units therefore.

Write the data you have in the form of a fraction. The units of the right side where m is distance meters and s is time seconds. A is a function of r and r is function of time so A can be written as a function of time also.

We can solve the second equation for quantity and substitute back into the first equation. We know that the equation for the circle is x 2 y 2 25. Our equation has three variables V r and h but we only have two derivatives dh and dV.

We can use related rates here if we want to observe the rates of change of the water levels height and volume with respect to time. And this the units here would be in radians per minute. θ d θ d t d y d t h d h d t y h 2.

V 25 196 π h 2 h V 25 196 π h 2 h. To find a relationship between the rates of change of x and y with respect to time we can implicitly differentiate the equation above with respect to t. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators.

Express the given information and rates look for units with time in the denominator 3. If possible draw a diagram to help visualize the problem. Quantity 01 c Revenue 2 c 0001 c 2.

Numerator divided by denominator. Which is the same thing as being equal to negative one fifth. Here are the general steps that can help you solve a related rates problem.

Step 1 Identify Known and Uknown Quantities. Consider on of those rising balloon related rates Calc problems. For example V t and r t for volume and radius with respect to time 4.

For example you say I drove 40 miles per hour Normally you dont say I drove 120 miles per 3 hours Figure out how to convert a rate like 120 miles per 3 hours to the unit rate of 40 miles per hour by watching this tutorial. We never actually refer to a specific. Here are the following steps in solving a related rates question.

If you have a rate such as price per some number of items and the quantity in the denominator is not 1 you can calculate unit rate or price per unit by completing the division operation. Revenue q 20 01 q 20 q 01 q 2 Cost 10 q. Writing Project 1.

Divide the total distance by the total time. We can find the function which defines its rate of change. We know that the equation for the circle is x 2 y 2 25.

D θ d t 1 s. When you talk about the speed of a car you usually say something in miles per hour. M s m m s m m 2 1 s.

Unit Rates Grade 7 Solutions Examples Worksheets Activities Videos

Calculus I Related Rates

Calculus I Related Rates

Share this post